Gridea

人脸识别损失函数

人脸识别损失函数
2022-11-09 · 10 min read
ML

人脸识别步骤

  1. 人脸检测
  2. 特征提取
  3. 特征对比

人脸识别的难点

  • 不同人脸类别之间的界限不是很明显
  • 脸与脸之间相似度很高，难以区分

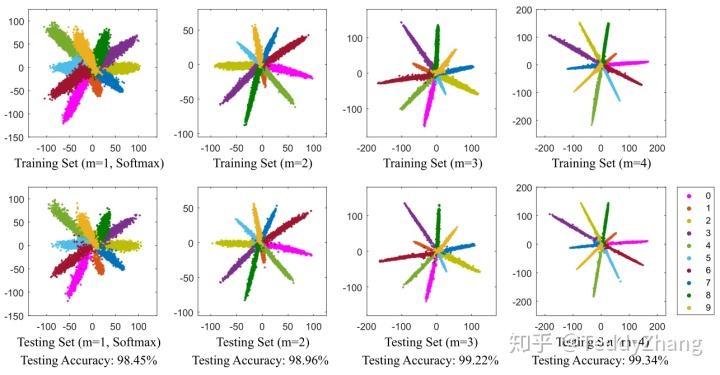
人脸识别损失函数

Softmax 和 Softmax Loss

Sj=eaj∑k=1TeakS_{j} = \frac{e^{a_{j}}}{\sum_{k=1}^{T}e^{a_{}k}}

aja_j 表示当前输入的类别特征
aka_k 表示从第1个到第T个类别特征

L=−∑j=1Tyjlog⁡SjL = - \sum_{j=1}^{T}y_{j}\log S_{j}

由于 yjy_{j} 是 0 或 1，公式简化为：

L=−log⁡SjL = -\log S_{j}

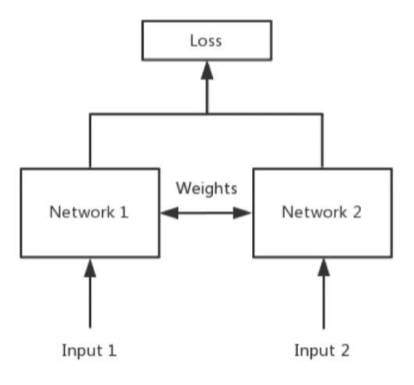
Siamese Network 孪生神经网络

Triplet Loss

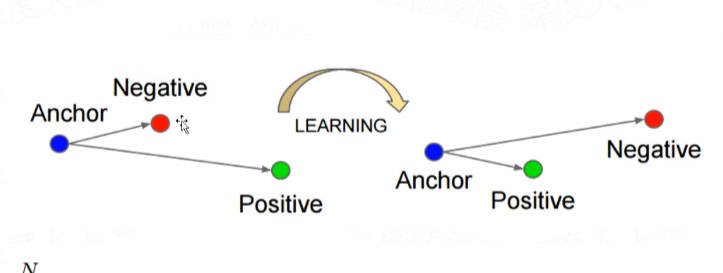
损失函数：
L=∑iN[∥f(xia)−f(xip)∥22−∥f(xia)−f(xin)∥22+α]L = \sum_{i}^{N}[\left \| f\left ( x_{i}^{a} \right ) - f\left ( x_{i}^{p} \right ) \right \|_{2}^{2} - \left \| f\left ( x_{i}^{a} \right ) - f\left ( x_{i}^{n} \right ) \right \|_{2}^{2}+ \alpha ]

对于二分类，从输出中随机挑选三个数据特征，两个为正样本特征，一个为负样本特征；
使用其中的一个正样本特征作为锚点，和另外两个特征做距离上的比较；
如果锚点和正样本特征的距离大于锚点和负样本特征的距离，就计算损失；反之，不需要计算损失

Center Loss 中心损失

在 softmax loss 基础上加入均方差损失

LC=12N∑i=1m∥xi−cyi∥22L_{C} = \frac{1}{2N} \sum_{i=1}^{m} \left \| x_{i}-c_{y_{i}} \right \|_{2}^{2}

xix_{i} 表示全连接层之前的特征
$c_{y_{i}} $ 表示第 $y_{i} $ 个类别的特征中心

Softmax loss 用于将类别分开
Center loss 用于将类别内数据集中

由于模型无法直接获得 c，所以将其放到网络里随机生成，在每一个 batch 里更新一次 c，然后将这个梯度形式的距离加到 center 上，做梯度下降。

∂CenterLoss∂x=1N∑i=1N(c−xi)\frac{\partial CenterLoss}{\partial x} = \frac{1}{N}\sum_{i=1}^{N}(c-x_{i})

在更新 center 的时候，加入 α\alpha 学习率，防止抖动

Δc=αN∑i=1N(c−xi)\Delta c = \frac{\alpha }{N}\sum_{i=1}^{N}(c-x_{i})

α\alpha 一般取 0.5

Center Loss 的缺点

  • 类别较多时，对硬件要求较高
  • L2 范数的离群点对 Loss 的影响较大
  • 个别类内距太大
  • 只适合同类样本差异不大的数据

Arcsoftmax

向量相关性的表示方法

  • 欧氏距离
  • 曼哈顿距离
  • 余弦相似度
    • 两个向量之间的角度越小，相似度系数越大，两个向量越相关；
    • 角度越大，相似度系数越小，越不相关。
    • 对绝对数值不敏感
    • 区分两个向量，最好的办法是增大角度 θ+m\theta+m，或者减小相似度系数 cos⁡(θ)−m\cos(\theta)-m
    • 余弦距离：1-余弦相似度

L-SoftmaxLoss

L4=1N∑i=1NLi=1N∑i=1N−log⁡(efyi∑jefi)L_{4}=\frac{1}{N} \sum_{i=1}^{N} L_{i}=\frac{1}{N} \sum_{i=1}^{N}-\log \left(\frac{e^{f_{y i}}}{\sum_{j} e^{f_{i}}}\right)

Li=−log⁡(e∥Wyi∣∥∣xi∥ψ(θyi)e∥Wyi∣∥xi∥ψ(θyi)+∑j≠yie∥Wj∥∥xi∥cos⁡(θj))L_{i}=-\log \left(\frac{e^{\left\|W _ { y i } \left|\left\|\mid x_{i}\right\| \psi\left(\theta_{y_{i}}\right)\right.\right.}}{e^{\left\|W_{y i} \mid\right\| x_{i} \| \psi\left(\theta_{y_{i}}\right)}+\sum_{j \neq y_{i}} e^{\left\|W_{j}\right\|\left\|x_{i}\right\| \cos \left(\theta_{j}\right)}}\right)

把其中的 cos⁡θ\cos \theta 改成了 cos⁡(mθ)\cos(m\theta)，

ψ(θ)={cos⁡(mθ),0⩽θ⩽πmD(θ),πm⩽θ⩽π\psi(\theta)=\left\{\begin{array}{c} \cos (m \theta), 0 \leqslant \theta \leqslant \frac{\pi}{m} \\ D(\theta), \frac{\pi}{m} \leqslant \theta \leqslant \pi \end{array}\right.

A-SoftmaxLoss

SoftmaxLoss 的输出

Li=−log⁡(eWyiTxi+byi∑jeWjTxi+bj)=−log⁡(e∥Wyi∥∥xi∥cos⁡(θyi,i)+byi∑je∥Wj∥∥xi∥cos⁡(θj,i)+bj)\begin{aligned} L_{i} &=-\log \left(\frac{e^{\boldsymbol{W}_{y_{i}}^{T} \boldsymbol{x}_{i}+b_{y_{i}}}}{\sum_{j} e^{\boldsymbol{W}_{j}^{T} \boldsymbol{x}_{i}+b_{j}}}\right) \\ &=-\log \left(\frac{e^{\left\|\boldsymbol{W}_{y_{i}}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{y_{i}, i}\right)+b_{y_{i}}}}{\sum_{j} e^{\left\|\boldsymbol{W}_{j}\right\|\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j, i}\right)+b_{j}}}\right) \end{aligned}

在训练过程中归一化权值 ∥w∥=1\left\|w\right\|=1 并且将偏置 biases 设置为 0

Lmodified =1N∑i−log⁡(e∥xi∥cos⁡(θyi,i)∑je∥xi∥cos⁡(θj,i))L_{\text {modified }}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{y_{i}, i}\right)}}{\sum_{j} e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j, i}\right)}}\right)

为了进一步将强特征的可判别性 ， 将角度系数 m(>1) 加入到损失函数中 ， 即 A-Softmax loss。
角度系数 m 一般是一个大于 1 的整数 。 所以 cos⁡(mθ)\cos(m\theta) 实际上是一个余弦倍角公式 。
当 m 增大时 ， 角度距离也会增加 ， 当 m=1 时 ， 角度距离为 0 。
A-Softmax loss 是一种增加角度乘积系数的方式来增大角分类的 。

Lang =1N∑i−log⁡(e∥xi∥cos⁡(mθyi,i)e∥xi∥cos⁡(mθyi,i)+∑j≠yie∥xi∥cos⁡(θj,i))L_{\text {ang }}=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(m \theta_{y_{i}, i}\right)}}{e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(m \theta_{y_{i}, i}\right)}+\sum_{j \neq y_{i}} e^{\left\|\boldsymbol{x}_{i}\right\| \cos \left(\theta_{j, i}\right)}}\right)

AM-SoftmaxLoss

用减小相似度系数的方式来增大向量之间的距离

根据 Normface, 对 f 进行归一化 ， 乘上缩放系数 s (默认超参 30)，最终的损失函数变为：

L6=−1m∑i=1mlog⁡es(cos⁡(θyi)−m)es(cos⁡(θyi)−m)+∑j=1,j≠yinescos⁡θjL_{6}=-\frac{1}{m} \sum_{i=1}^{m} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}\right)-m\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}\right)-m\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}}

这样做的好处在于 A-Softma× 的倍角计算是要通过倍角公式 ， 反向传播时不方便求导 ， 而只减 m 反向传播时导数不用变化
公式里第一个 m 是批次，第二个 m 是超参数
A-Softmax 是用 m 乘以 θ\theta, 而 AM-Softmax 是用 cos⁡θ\cos\theta 减去 m, 这是两者的最大不同之处：一个是角度距离，一个是余弦相似度距离。

Arc-SoftmaxLoss

根据 cos 的性质 ， 优化角度距离比优化余弦距离更有效果 ， 因为余弦距离相对更密集。
公式里第一个 m 是批次 ， 第二个 m 是超参数
增大角度比减小相似度距离对分类的影响更加直接，所以可以改为直接增加角度的方式。

注意 ： 反三角余弦计算出来的是弧度 ， 而非角度 。 所以实际增加的 m 也是增加的弧度。

LArcFaceLoss=−1m∑i=1mlog⁡es(cos⁡(θyi+m))es(cos⁡(θyi+m))+∑j=1,j≠yinescos⁡θjL_{ArcFaceLoss}=-\frac{1}{m} \sum_{i=1}^{m} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}}

课件